Sudoku Beispiel 1 (schwer)
Dieses Beispiel ist ein sehr schönes, aber auch sehr schweres Sudoku-Rätsel. Die ganze Bandbreite der Sudoku-Strategien wird hier sehr schön abgebildet. Neben einigen fortgeschrittenen Methoden können hier die folgenden Lösungsstrategien verwendet werden:
- X-Wing
- 4 x Widerspruchstechnik (Rectangle Elimination)
- 2 x XY-Wing
- XYZ-Wing
- WXYZ-Wing
- XY-Kette
Nun aber zum Sudoku. Das Ausgangsrätsel sieht wie folgt aus:
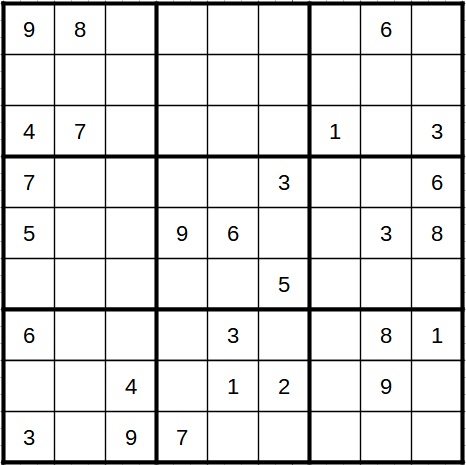
Auf dem Weg zum zweiten Bild habe ich ein paar Schritte übersprungen, da ich mich hier vor allem auf die schweren Strategien konzentrieren will. Es handelt sich hier immer um eindeutige Kandidaten, was natürlich nicht heißt, dass man sie alle sofort sieht.
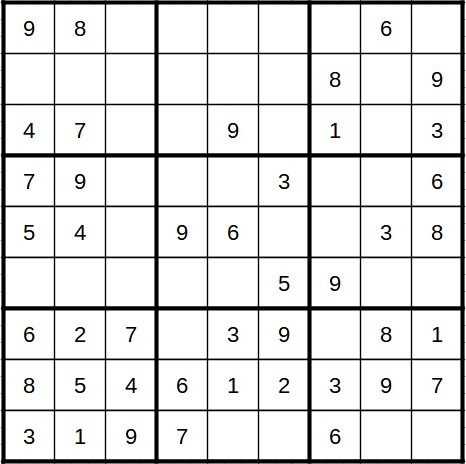
Im nächsten Schritt sehen wir in einem Block einen direkten zweifachen Kandidaten. Dieser ist hier grün markiert. Wir können also die anderen Kandidaten 1 und 2 aus anderen Feldern des gleichen Blocks streichen.
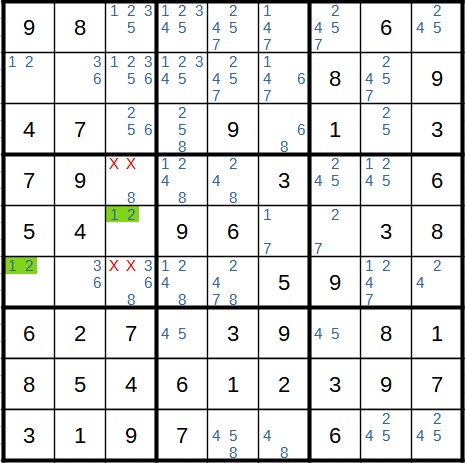
Jetzt kommt die erste schwierige Technik. Zum ersten von vier Malen kann hier die Widerspruchstechnik (Rectangle Elimination) eingesetzt werden. Hier gehen wir vom fünften Feld in der ersten Zeile aus. Würde dort eine 7 stehen, fiele diese in der gleichen Zeile ansonsten überall weg. Sie würde dann nur noch in dem gelb markierten Feld weiter unten für diese Spalte in Frage kommen. Die 7 würde also im Startfeld und im Zielfeld stehen. Das hätte aber zur Folge, dass im Block in der Mitte die 7 in keinem Feld mehr als Kandidat vorkommen könnte. Das ist ein Widerspruch zu den Sudoku-Regeln und die 7 kann daher aus dem Startfeld gestrichen werden.
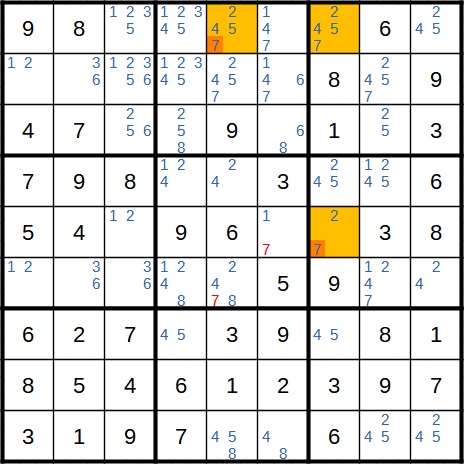
Nun liegt ein X-Wing in den rot markierten Spalten vor. Hier geht es um die 7, die dort nur in zwei verschiedenen Zeilen vorkommt. Die 7 können wir in der zweiten Zeile dann als Kandidat streichen.
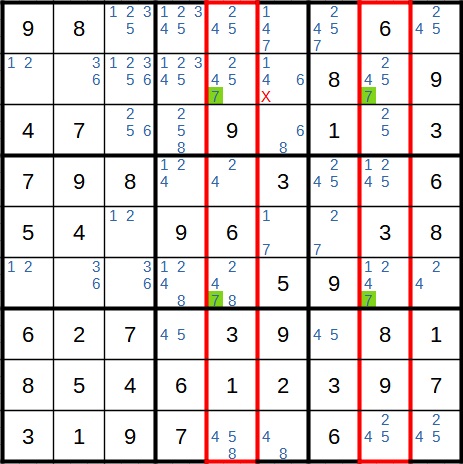
Danach können wir wieder die Widerspruchstechnik anwenden. Hier ist das vierte Feld der ersten Zeile das Startfeld. Steht dort die 5, steht sie auch unten rechts. Das führt zu einem Widerspruch im Feld unten in der Mitte. Daher kann die 5 nicht im Startfeld stehen.
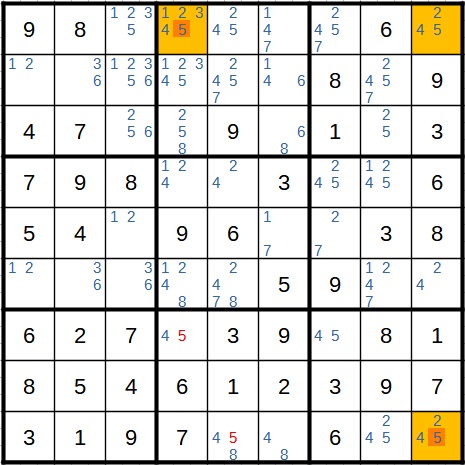
Auch im nächsten Schritt haben wir wieder einen Widerspruch. Hier würde im Block links oben die 1 nicht vorkommen können. Also kann die 1 im Block oben in der Mitte aus dem gelben Feld wegfallen.
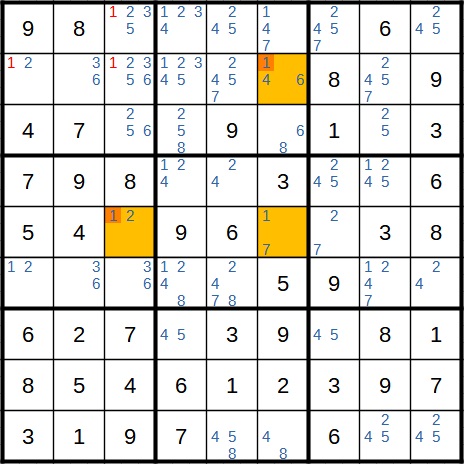
Als nächstes haben wir einen direkten dreifachen Kandidaten (4, 6 und 8) in der sechsten Spalte. Also können wir eine 4 weiter oben streichen.
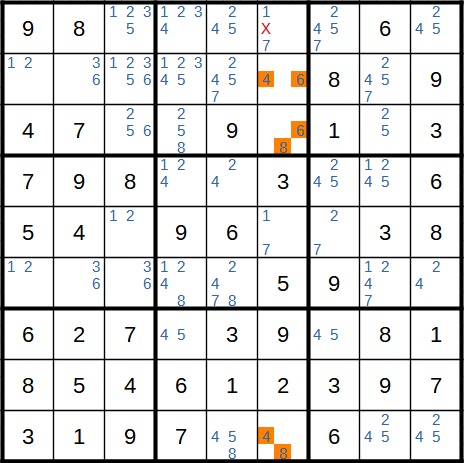
Jetzt wird es ziemlich knifflig. Denn hier liegt ein (etwas versteckter) WXYZ Wing vor. Dieser ist deshalb als WXYZ-Wing so schwer zu identifizieren, da im Startfeld (hellgrün markiert) nur zwei Ziffern vorkommen. Allerdings haben wir insgesamt vier verschiedene Ziffern: 1, 2, 4 und 7. Der einfachere Fall ist der, in dem im Startfeld die 7 steht. Dann steht im gelben Feld rechts daneben die 2. Andernfalls steht im Startfeld die 1 und damit fällt im Feld links oben im gleichen Block die 1 als Kandidat weg. Damit hätten wir nebeneinander in zwei Feldern einen Zwilling (2 und 4). Auch in diesem Fall würde die 2 in der gleichen Zeile an anderen Stellen wegfallen. Für zwei Felder fällt die 2 also in beiden Fällen weg. Also kann sie ganz gestrichen werden. Ich selbst habe diese Taktik übrigens nicht gesehen, sondern wurde erst darauf aufmerksam, nachdem ich die Situation online in einen Sudoku-Löser eingegeben hatte.
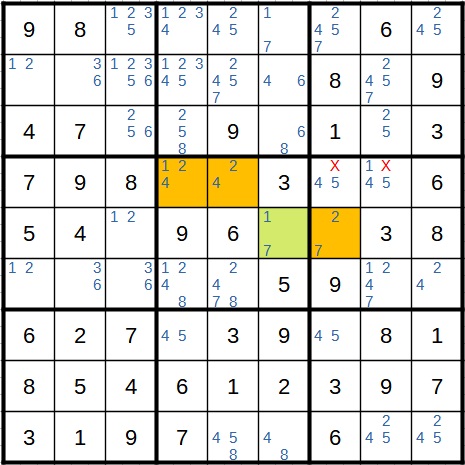
Im nächsten Schritt wird es wieder etwas einfacher. Hier liegt ein Zwilling (4 und 5) in der siebten Spalte vor. Also fallen beide Ziffern weiter oben in der Spalte einmal weg.
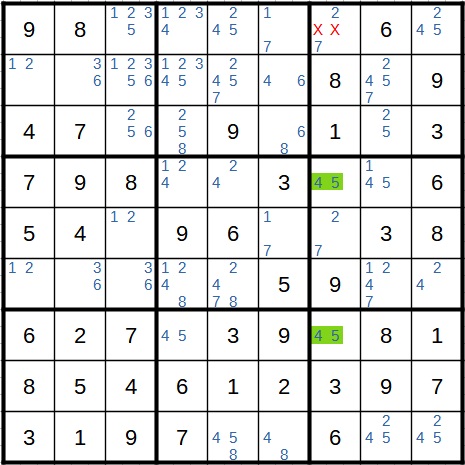
Nun kann eine weitere fortgeschrittene Taktik angewendet werden, nämlich die Methode der eingeschlossenen Kandidaten. In der rot markierten Zeile ist der Kandidat 2 auf den mittleren Block beschränkt und muss daher auch in einem dieser beiden Felder stehen. Weiter unten im Block streichen wir daher die 2.
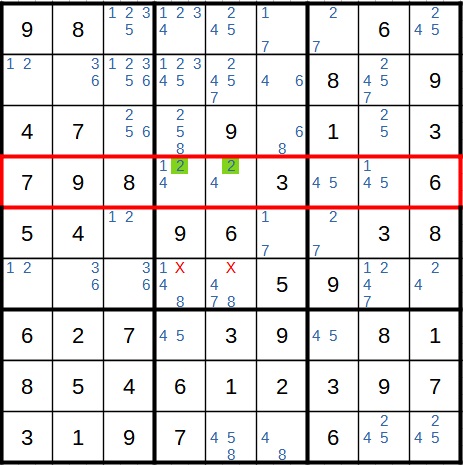
Danach können wir zum vierten und letzten Mal die Widerspruchstechnik heranziehen. Hier ist das Startfeld unten rechts. Haben wir dort die 4, steht diese auch im Zielfeld. Das führt zu einem Widerspruch im Block oben rechts, wo jede 4 wegfallen würde.
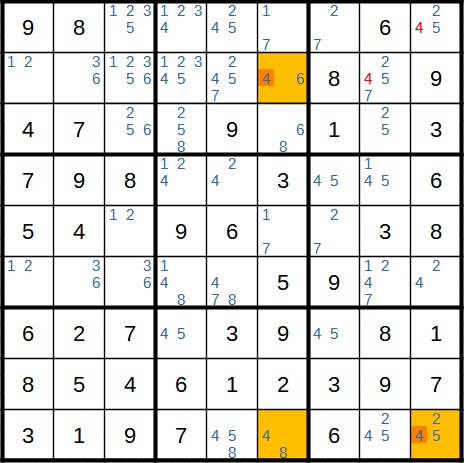
Im nächsten Schritt können wir zum ersten Mal einen XY Wing anwenden. Hier ist das Ausgangsfeld wieder hellgrün markiert. Im ersten Fall steht dort eine 2. Dann steht unten rechts eine 5. Im zweiten Fall ist im Ausgangsfeld eine 4, woraus eine 5 im gelben Feld oben links davon folgt. Im Block rechts unten würde also in beiden Fällen in einem der Felder die 5 wegfallen. Also streichen wir sie dort auch. Danach bleibt dort nur noch die 4 übrig (und wir können außerdem zweimal die 5 fest eintragen).
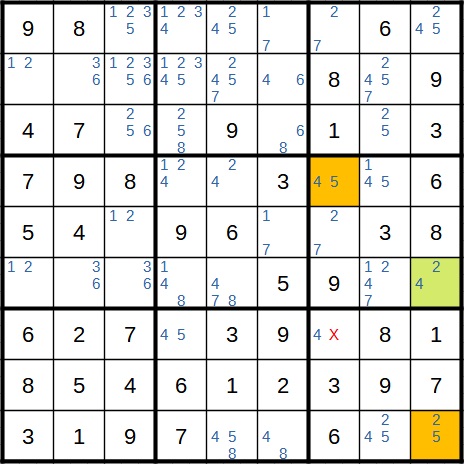
Jetzt haben wir wieder einen direkten doppelten Kandidaten (2 und 5). Also können diese in der gleichen Spalte an anderen Stellen wegfallen.
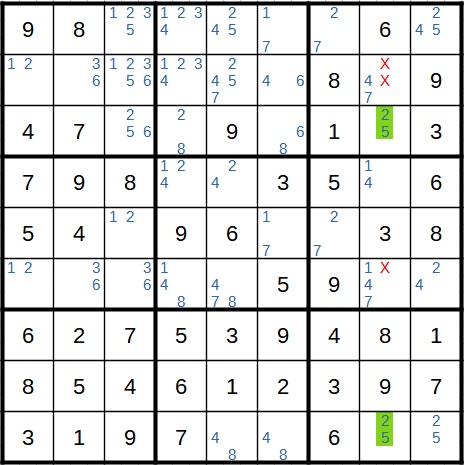
Als nächstes kommt zum zweiten Mal der XY-Wing ins Spiel. Hier ist wie oben das Startfeld wieder grün gefärbt. In beiden Fällen haben wir in einem der gelben Felder die 1, also fällt sie im Feld links vom Startfeld weg, da dieses mit beiden Feldern verbunden ist. Damit bleibt im Block mit dem Startfeld nur noch für das gelbe Feld die 1 übrig und wir können sie fest dort eintragen.
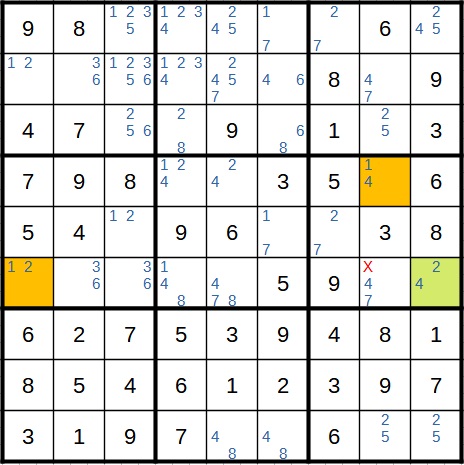
Anschließend kommt wieder ein Zwilling vor, nämlich die 2 und die 4 in der vierten Spalte. Die 4 fällt dadurch an zwei anderen Stellen weg. Man hätte diese Situation auch als eingeschlossenen Kandidaten interpretieren können, mit dem gleichen Ergebnis.
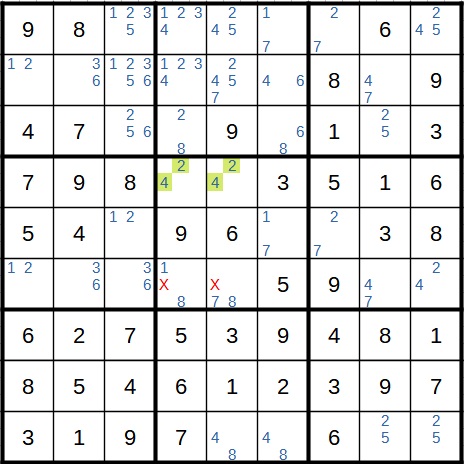
Als nächste schwere Sudoku-Strategie kann eine XY-Kette identifiziert werden. Das Startfeld ist hier grün und das Zielfeld orange markiert. Haben wir im Startfeld eine 2, folgt daraus über die beiden gelben Zwischenfelder eine 4 im Zielfeld. Andernfalls steht die 4 im Startfeld. In beiden Fällen würde in zwei anderen Feldern die 4 als Kandidat wegfallen.
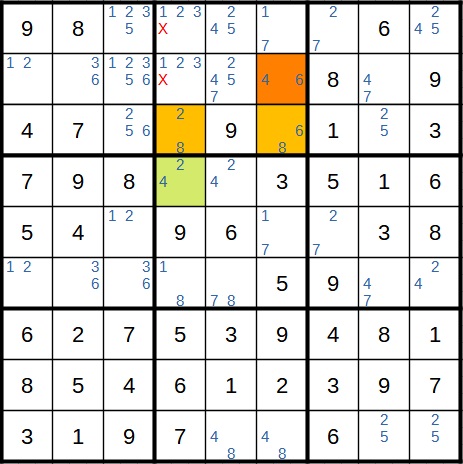
Zur Krönung gibt es dann als letzte schwere Strategie noch einen XYZ Wing. Auch hier ist das Startfeld wieder hellgrün. In den drei Fällen steht entweder im Startfeld oder einem der beiden gelben Felder eine 4. In einem Feld fällt dann die 4 weg. Dort bleibt nur noch die 6 und auch andere Felder können gelöst werden.
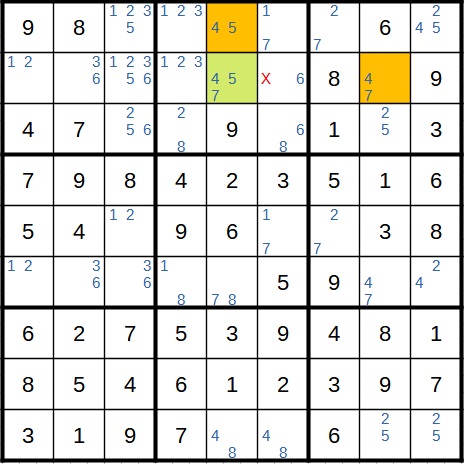
Ab jetzt gibt es keine größeren Hindernisse mehr. Die Lösung sieht wie folgt aus:
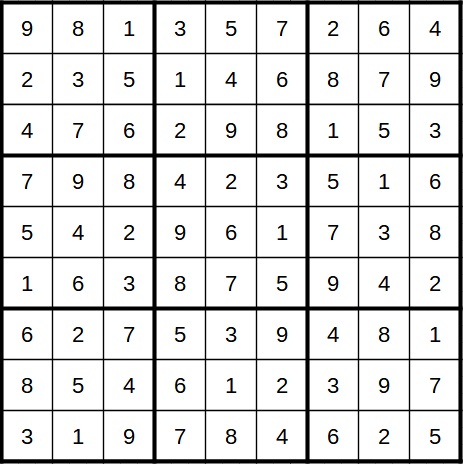
Das ist natürlich ein ziemlich extremes Beispiel aufgrund der reinen Anzahl an Techniken, die man anwenden kann. Aber es zeigt gut die Vielfalt der Strategien. Ich selbst konnte dieses Rätsel wie gesagt nicht ohne Hilfe lösen. Aber vor allem der Schritt mit dem WXYZ-Wing war überraschend und ich werde in Zukunft wohl etwas genauer bei solchen Situationen hinschauen.