XY-Wing (XY-Flügel)

Der XY-Wing erinnert vom Begriff her etwas an den X-Wing. Es liegt hier aber ein anderes Prinzip vor, auch wenn es in einer Variante ähnlich aussieht. Vielmehr baut diese Methode auf einer Auswirkungskette auf. Manchmal wird der XY-Wing auch einfach als Y-Wing bzw. Y-Flügel bezeichnet.

Wie funktioniert der XY-Wing?

Zur Erläuterung schauen wir uns das folgende Schaubild an.

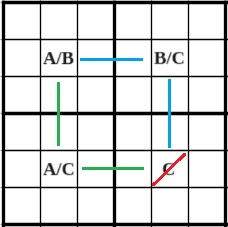
In dieser Variante sieht es tatsächlich aus wie ein X-Wing, denn es liegt hier ein Rechteck vor. Das Startfeld ist das Feld mit A und B als Kandidaten. Steht in diesem Feld ein A, steht im A/C-Feld ein C. Steht im Startfeld jedoch ein B, steht im B/C-Feld ein C. Da das Startfeld aber nur A und B als mögliche Kandidaten hat, gibt es keinen anderen Fall. In beiden Fällen kann in dem Feld, das an das A/C-Feld und das B/C-Feld grenzt (hier durch das durchgestrichene C veranschaulicht), kein C stehen. Denn sonst würde in der gleichen Zeile oder Spalte ja zweimal ein C stehen, was den Sudoku-Regeln widerspricht. Also streichen wir das C als Kandidaten.

Ein XY-Wing muss aber nicht in dieser Rechtecks-Formation vorliegen. In einer anderen Form kann es sogar noch hilfreicher sein, da mehr Felder erreicht werden. Auch hierzu ein Schaubild:

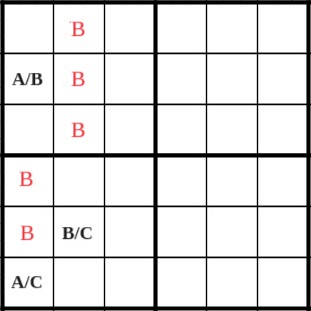
Jetzt gehen wir nach der gleichen Logik wie oben vor. Hier starten wir mit dem A/C-Feld. Steht im A/C-Feld ein A, steht im A/B-Feld ein B. Ist hingegen im A/C-Feld ein C, muss das B im B/C-Feld stehen. Das B steht also in beiden Fällen in einem der beiden Felder. Und mehr als zwei Fälle gibt es nicht. In allen durch das rote B markierten Feldern kann das B als Kandidaten gestrichen werden. Denn all diese Felder liegen in der gleichen Spalte und dem gleichen Block wie das A/B-Feld bzw. das B/C-Feld.

Beispiele für XY-Wing

Schauen wir uns hierzu zwei Beispiele an und beginnen mit der zweiten Variante (ohne Rechtecksform).

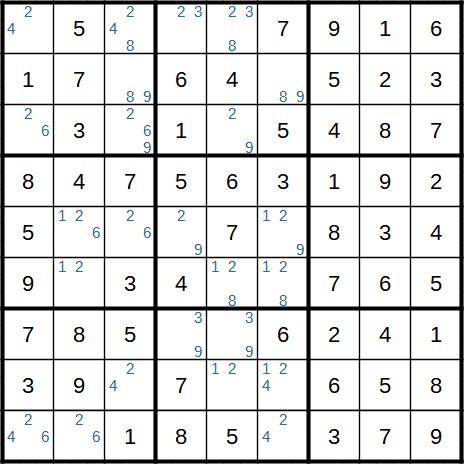
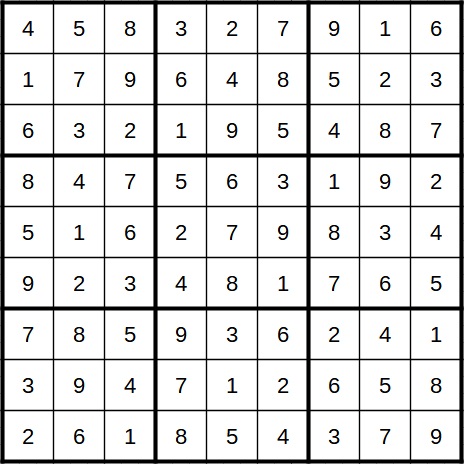
Hier ist das Startfeld grün markiert und die beiden Zwischenfelder gelb. Steht im Startfeld die 2, steht im Zwischenfeld im gleichen Block die 9. Falls jedoch im Startfeld die 3 steht, haben wir im Zwischenfeld in der gleichen Spalte eine 9. In den Feldern, die an beide diese Zwischenfelder grenzen, kann daher die 9 als Kandidat gestrichen werden. Das ist in einem Feld der Fall.

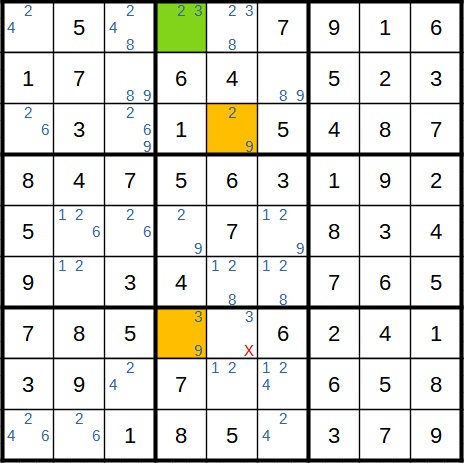
Als Bonus kommt hier dazu, dass im „Zielfeld“ nun nur noch die 3 als Kandidat bleibt und fest dort eingetragen werden kann. Dadurch lässt sich das Sudoku komplett lösen.

Anschließend noch ein Beispiel in der X-Wing-Form.

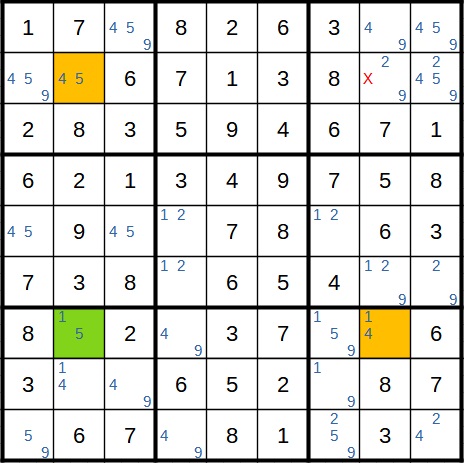
Dort ist das Startfeld wieder grün markiert und die beiden Zwischenfelder gelb. In beiden Fällen steht in einem der Zwischenfelder ein 4. Also kann die 4 im Zielfeld als Kandidat wegfallen.

Das Prinzip des XY-Wings kann jetzt übertragen werden auf den XYZ-Wing und den WXYZ-Wing. Beiden liegt dieselbe Logik zugrunde, auch wenn es Unterschiede gibt.