WXYZ-Wing (WXYZ-Flügel)

Wir haben bereits gesehen, dass der XYZ-Wing eine Weiterentwicklung des XY-Wing ist. An dieser Stelle können wir das ganze aber noch etwas weiterführen und eine weitere Ziffer hinzufügen. Das Ganze nennt man dann WXYZ-Wing. Hierzu ein Schaubild zur besseren Verständlichkeit.

Wie funktioniert der WXYZ-Flügel?

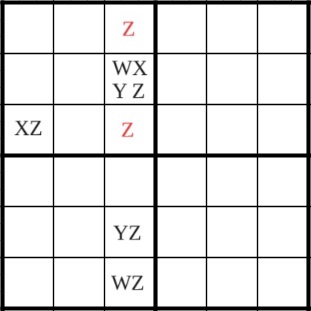
Im obigen Schaubild haben wir ein Feld, das die Kandidaten W, X, Y und Z enthält. Dieses bezeichnen wir wieder als Startfeld. Hier gibt es nun vier verschiedene Fälle.

Fall 1: Startfeld enthält das W. Dann steht im W/Z-Feld das Z.

Fall 2: Startfeld enthält das X. Dann steht im X/Z-Feld das Z.

Fall 3: Startfeld enthält das Y. Dann steht im Y/Z-Feld das Z.

Fall 4: Startfeld enthält das Z.

In allen Fällen steht in einem der Felder ein Z. Die Felder mit dem roten Z im obigen Schaubild grenzen an alle diese Felder über Block und/oder Spalte. In diesen Feldern kann daher nicht noch ein weiteres Z stehen.

Allerdings muss der WXYZ-Wing nicht in dieser Formation vorliegen. Wichtig ist nur, dass insgesamt vier verschiedene Kandidaten vorkommen. Aber das Startfeld z.B. hätte nicht alle vier Kandidaten enthalten müssen. Nehmen wir beispielsweise an, dass das Startfeld nur X, Y und Z enthalten würde. Dann gäbe es nur drei Fälle. Aber in jedem der drei Fälle hätten wir in einem der Zwischenfelder ein Z. Das Endergebnis wäre also gleich.

Es ist auch möglich, dass die Zwischenfelder sich gegenseitig beeinflussen. Das wird im Beispiel unten deutlich.

Beispiele für den WXYZ-Wing

Ein WXYZ-Wing kommt in der Realität ziemlich selten vor. Allerdings kann er sehr hilfreich sein. Das folgenden Beispiel enthält zwei Situationen, in denen man die Strategie anwenden kann.

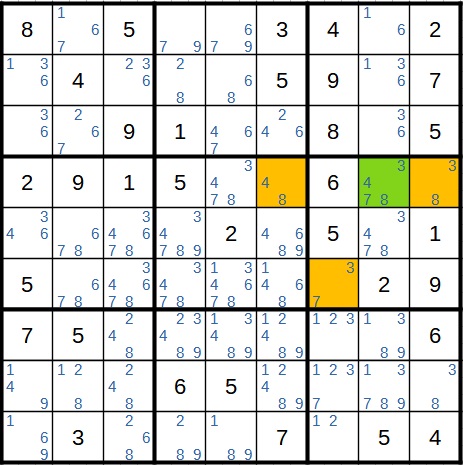
Die vier Kandidaten sind 3, 4, 7 und 8. Das Startfeld ist grün markiert. Steht im Startfeld die 3, steht im 3/8-Feld die 8. Aus der 4 im Startfeld folgt die 8 im 4/8-Feld. Die 7 im Startfeld führt zur 3 im 3/7-Feld, was dann wiederum zur 8 im 3/8-Feld führt. Im vierten Fall steht die 8 im Startfeld. Hier ist die 8 der Kandidat, der in jedem der vier Fälle vorkommt. In einem Feld können wir diesen Kandidaten also streichen.

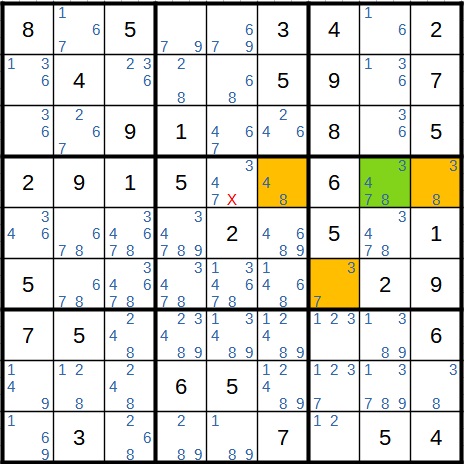
Oben habe ich ja bereits erwähnt, dass nicht alle vier Kandidaten im Startfeld stehen müssen. Wer ganz genau hingeschaut hat, wird diesen Fall vielleicht auch hier beobachtet haben. Denn im Block oben rechts hätten wir vorher die Methode der eingeschlossenen Kandidaten anwenden können. Die 1, 3 und 6 stehen in dieser Spalte zwingen an diesen drei Stellen (alle anderen Stellen des Blocks sind ja bereits belegt). Daher kann man diese Kandidaten an allen anderen Stellen der gleichen Spalte wegstreichen. Das gilt auch für die 3 im Startfeld. In dieser Situation hätte es nur drei Fälle gegeben, aber am Ergebnis hätte sich nichts geändert.

Anschließend liegt in dieser Beispiel noch ein weiterer WXYZ-Wing vor. Dieser ist im folgenden Bild zu sehen.

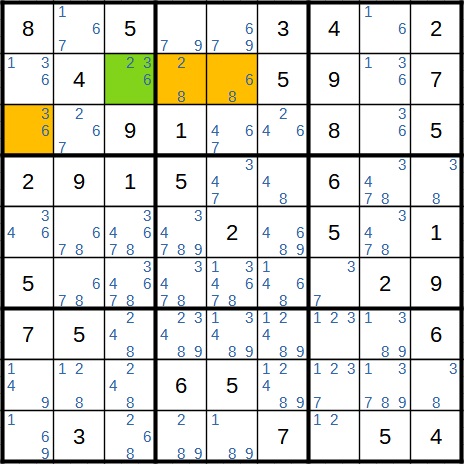
Hier enthält das Startfeld von Beginn an nur drei der vier Kandidaten. Die vier Kandidaten sind 2, 3, 6 und 8. In dieser Situation müssen wir nur drei Fälle betrachten.

Fall 1: Startfeld hat den Wert 2, dann steht im 2/8-Feld die 8 und im 6/8-Feld die 6.

Fall 2: Startfeld hat den Wert 3, dann steht im 3/6-Feld die 6.

Fall 3: Startfeld hat den Wert 6.

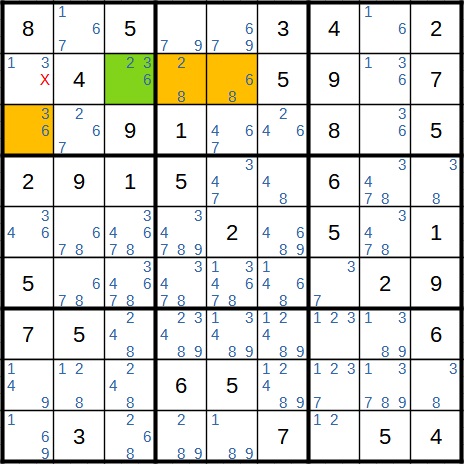
Da in allen Fällen eine 6 in einem der Felder steht, kann diese in einem anderen Feld als Kandidat wegfallen.

In diesem Beispiel stand die 8 nicht im Startfeld. Sie hatte aber eine wichtige Funktion in Fall 1 und ohne sie hätte das Ganze nicht funktioniert.

Dies war die letzte dieser Art von Strategien. Rein theoretisch könnte man das Prinzip noch auf fünf Kandidaten ausweiten und diese Methode dann wohl VWXYZ-Wing nennen. Allerdings ist mir eine solche Situation noch nie begegnet.