Versteckter dreifacher Kandidat
Die Methode des versteckten dreifachen Kandidaten baut auf der Methode der versteckten zweifachen Kandidaten und der Methode der direkten dreifachen Kandidaten auf. Man sucht in drei verschiedenen Feldern innerhalb einer Zeile, einer Spalte und/oder eines Blocks einen Drilling. Dieser ist aber versteckt, da in den drei Feldern neben den Drillingskandidaten noch weitere Kandidaten auftauchen. Auch dies wird anhand eines Beispiels klarer.

Beispiel zum versteckten dreifachen Kandidaten
Hier geht es um die rot markierte Spalte. Die Kandidaten sind 2, 6 und 9. Diese drei Kandidaten kommen nur in drei verschiedenen Feldern vor.
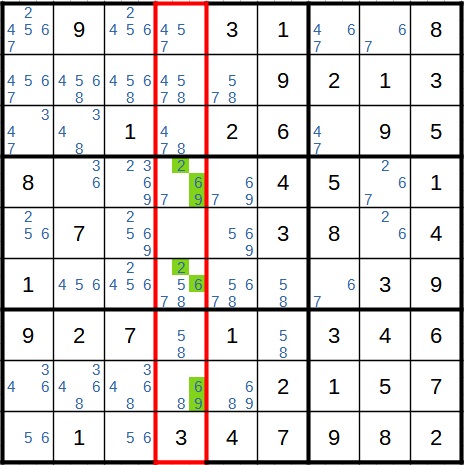
Da weder die 2 noch die 6 noch die 9 in einem anderen Feld derselben Spalte vorkommen, stehen sie zwangsläufig – in welcher Reihenfolge auch immer – in den markierten Feldern. Daher kann aus diesen Feldern jeder andere Kandidat gestrichen werden. Auch hier sei noch einmal daran erinnert, dass nicht jeder der drei Kandidaten auch in jedem der drei Felder vorkommen muss. In unserem Beispiel kommen nur in einem der Felder die 2, die 6 und die 9 alle vor. Zwei der drei Kandidaten reichen aber aus. Der wichtige Punkt ist, dass die 2, die 6 und die 9 am Ende nur in diesen drei Feldern stehen können. Sie können weder in einem der anderen sechs Felder stehen noch kann eine andere Zahl (beispielsweise die 8) in eines unserer drei Felder eingetragen werden.
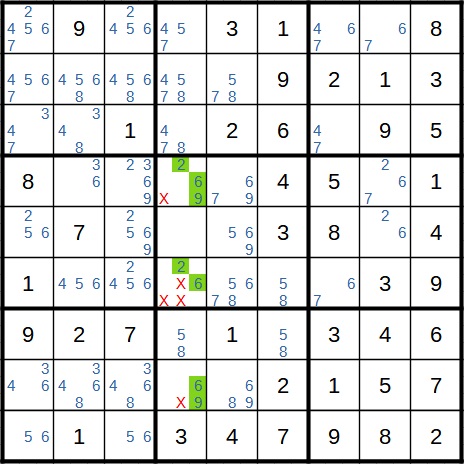
Prinzip ist theoretisch noch erweiterbar
Dieses Prinzip ließe sich jetzt wie gesagt auch noch auf vier Kandidaten übertragen. Eine solche Situation kommt aber in der Realität äußerst selten vor. Bzw. liegt eine andere Variante zur gleichen Zeit vor. Hierzu können wir uns das Beispiel anschauen, dass ich auch schon beim direkten dreifachen Kandidaten verwendet habe.
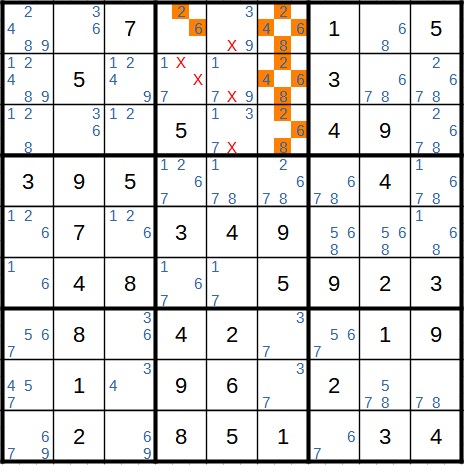
Hier bilden die 2, die 4, die 6 und die 8 einen direkten vierfachen Kandidaten. Man hätte natürlich auch komplizierter vorgehen und 1, 3, 7 und 9 als versteckten vierfachen Kandidaten identifizieren können. Allerdings müsste man dafür den direkten Weg übersehen, aus dem der indirekte (versteckte) unmittelbar folgt.
In der Regel wird man bei fortgeschrittenen bzw. mittelschweren Sudoku mit diesen Methoden der direkten bzw. versteckten Mehrfach-Kandidaten sowie der Methode der eingeschlossenen Kandidaten aber bereits einiges erreichen können.