Methode der eingeschlossenen Kandidaten

Die Methode der eingeschlossenen Kandidaten ist eine fortgeschrittene Sudoku-Strategie, bei der man die Kandidatenschreibweise zur Hilfe verwendet. Hier geht es darum, dass in jeder Zeile, jeder Spalte und in jedem Block ein Kandidat nur genau einmal vorkommt.

In manchen Fällen kann die Stelle, an der ein Kandidat stehen muss, auf einen Teilbereich der Zeile, Spalte oder des Blocks eingeschränkt werden. Dann kann der Kandidat an anderen Stellen außerhalb dieses Teilbereichs gestrichen werden. Dies wird anhand von Beispielen deutlicher. Zunächst aber kann die Strategie der eingeschlossenen Kandidaten auf drei verschiedene Weisen definiert werden.

Methode 1 (Zeile):
Ist innerhalb einer Zeile ein Kandidat auf einen Block beschränkt, kann man ihn an anderen Stellen des Blocks als möglichen Kandidaten streichen.

Methode 2 (Spalte):
Ist innerhalb einer Spalte ein Kandidat auf einen Block beschränkt, kann man ihn an anderen Stellen des Blocks als möglichen Kandidaten streichen.

Methode 3 (Block):
Ist innerhalb eines Blocks ein Kandidat auf eine Zeile oder Spalte beschränkt, kann man ihn an anderen Stellen der Zeile oder Spalte als möglichen Kandidaten streichen.

Beispiel zu Methode 1 (Zeile)

Wir beginnen mit einem Beispiel für Methode 1. Hier betrachten wir die mittlere Zeile. In dieser kommt der Kandidat 7 nur im Block ganz rechts vor.

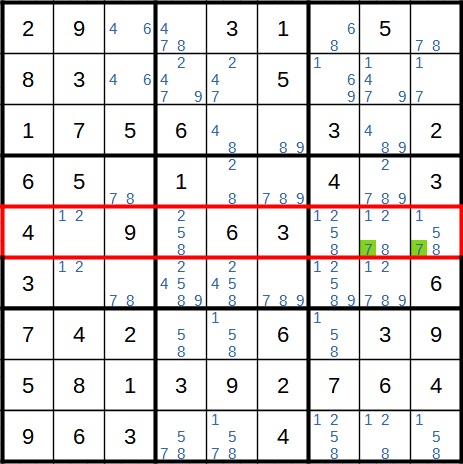
Die 7 ist innerhalb der Zeile also sozusagen im rechten Block eingeschlossen. Daher der Name Methode der eingeschlossenen Kandidaten. Da aber jede Zeile, jede Spalte und jeder Block jede Zahl von 1 bis 9 nur genau einmal enthält, kann die 7 in der Zeile bzw. dem Block auch nur an den grün markierten Stellen stehen. Sie kann daher an allen anderen Stellen des Blocks als Kandidat gestrichen werden.

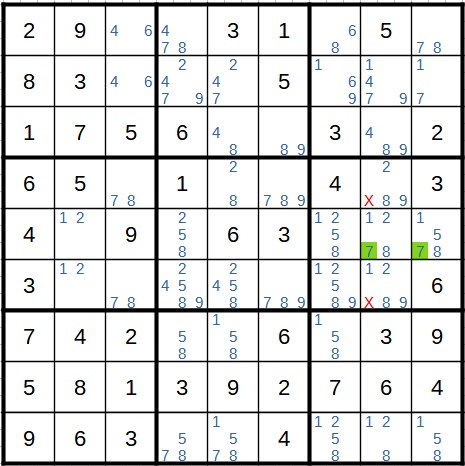
Beispiel zu Methode 2 (Spalte)

Hier wenden wir die gleiche Logik an wie oben, nur mit einer Spalte statt einer Zeile. In der rot umrandeten Spalte kommt der Kandidat 2 ausschließlich im mittleren Block vor.

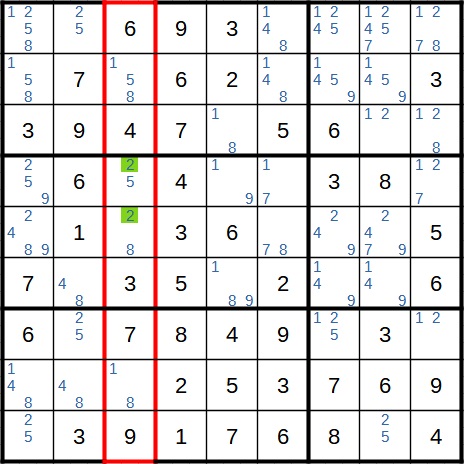
Daher muss die 2 auch an einer dieser beiden Stellen stehen. Andernfalls würde die dritte Spalte keine 2 enthalten. Und dann wäre das Sudoku fehlerhaft bzw. gar kein Sudoku. Wir streichen also die 2 an anderen Stellen des Blocks als Kandidat.

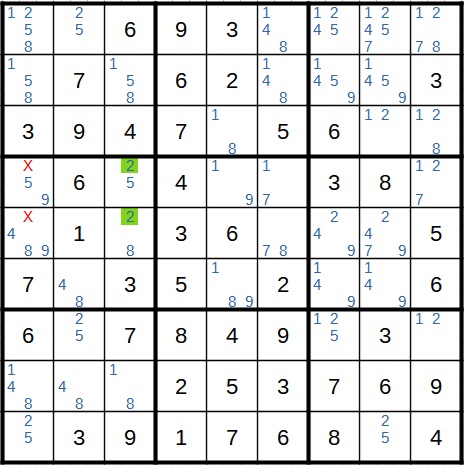
Beispiel zu Methode 3 (Block)

Zum Abschluss noch ein Beispiel zu Methode 3. Hier haben wir im Block rechts oben die 3 als Kandidat nur in der äußeren Spalte. Die 3 ist also in dieser Spalte eingeschlossen.

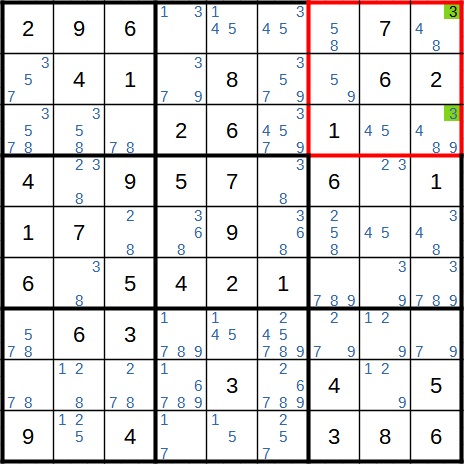
Nach der gleichen Logik wie oben kann die 3 also an allen anderen Stellen der Spalte als Kandidat wegfallen.

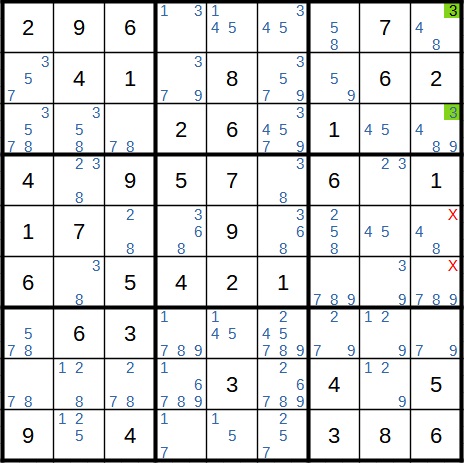
Anwendung der Methode der eingeschlossenen Kandidaten

Die Methode der eingeschlossenen Kandidaten wird häufig verwendet, nachdem man mit einfachem Scannen nicht mehr weitergekommen ist und daher die möglichen Kandidaten in die noch offenen Felder eingetragen hat. Auf diese Weise versucht man, die Anzahl der Kandidaten zu reduzieren. Hat ein Feld nur zwei mögliche Kandidaten und einer davon wird aufgrund der Methode der eingeschlossenen Kandidaten gestrichen, kann eine Zahl sogar direkt eingetragen werden.

Oftmals wird das Bild hierdurch aber nur vereinfacht, bevor die wirklich schwierigen Methoden angewendet werden. In der Regel arbeitet man sich hier Schritt für Schritt durch. Beispielsweise betrachtet man zuerst alle neun Blöcke und sucht nach eingeschlossenen Kandidaten. Anschließend dann die neun Zeilen und neun Spalten. Hat man nach einem Durchgang Kandidaten streichen können, kann der ganze Vorgang von vorne losgehen. Denn durch das Streichen hat sich natürlich die Gesamtsituation geändert. Es könnte jetzt eingeschlossene Kandidaten geben, die vorher noch nicht da waren.