Widerspruchstechnik (Rectangle Elimination)
Die Widerspruchstechnik in Sudoku erinnert an Auswirkungsketten. Auch hier starten wir in einem bestimmten Feld, nehmen einen Wert für dieses Feld an und schauen uns an, welche Auswirkungen das hat. Hier liegt aber ein besonderer Fall vor.
Diese Technik wird im Englischen auch gerne als Rectangle Elimination bezeichnet. Rectangle bedeutet im Deutschen Rechteck. Wenn wir uns die Beispiele weiter unten angeschaut haben, wird klar, warum diese Bezeichnung verwendet wird. Würden wir alle Felder miteinander verbinden, die hier betroffen sind, würde sich ein Rechteck ergeben. Was die Form betrifft gibt es also auch Gemeinsamkeiten mit einem X-Wing.
Aber wie funktioniert die Widerspruchstechnik (Rectangle Elimination) nun?
Das ist mit Worten nicht einfach zu erklären. Daher werden wir uns weiter unten zwei Beispiele zu dieser Sudoku-Strategie anschauen, um das Ganze zu veranschaulichen.
Im Grunde genommen haben wir drei Felder, die wir betrachten. Wir nehmen für eines dieser Felder an, dass es einen bestimmten Kandidaten enthält. Anschließend schauen wir, welche Auswirkung das auf die beiden anderen Felder hat und - was noch wichtiger ist - auf andere Felder innerhalb eines bestimmten Blocks. Wie gesagt würde sich eine Rechtecksform ergeben, wenn wir all diese Felder verbinden.
Ziel ist es nun, einen Widerspruch zu den Sudoku-Regeln zu finden. In diesem Fall wäre das beispielsweise wie folgt: Würde im Startfeld der Kandidat 2 stehen, wäre in einem Block der Kandidat 4 für alle noch leeren Felder ausgeschlossen. Jeder Block muss aber jede Zahl von 1 bis 9 genau einmal enthalten, also auch die 4. Die 2 im Startfeld würde also zu einem Widerspruch führen. Aus diesem Grund nenne ich diese Strategie ganz allgemein Widerspruchstechnik. Stoßen wir auf einen solchen Widerspruch, können wir einen Kandidaten ausschließen.
Dies ist aber in Textform schwierig zu verstehen, daher nun zwei Beispiele.
Beispiele für Widersprüche in Sudoku
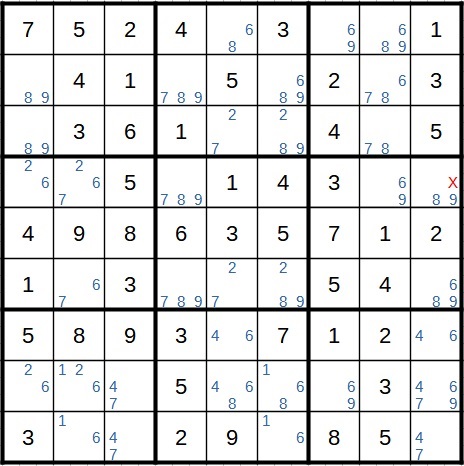
Schauen wir uns das folgende Spielfeld an. Ich habe die wichtigen Felder schon einmal gelb markiert. Es geht hier im Feld links oben um den Kandidaten 5.
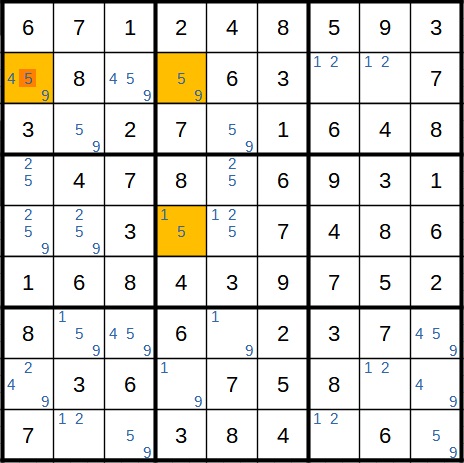
Was geschieht nun, wenn dort die 5 stehen würde? In diesem Fall würde im gelben Feld rechts daneben eine 9 stehen und im gelben Feld unterhalb davon auch eine 5 (da unten in der selben Spalte dann eine 1 steht). Wir schauen uns nun die Auswirkungen auf den Block links mittig an, da dieser an diese Felder grenzt. Die beiden gelben Felder mit der 5 nennen wir Start- bzw. Zielfeld.
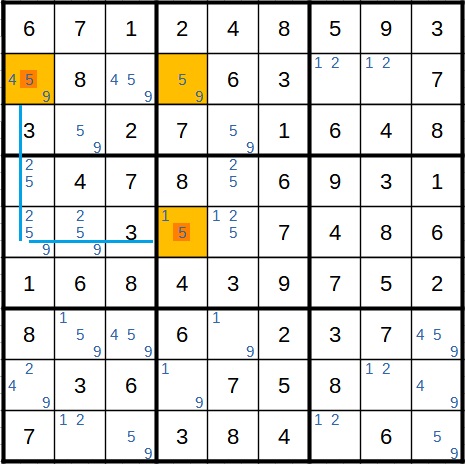
Da im Startfeld eine 5 steht, kann diese in der ersten Spalte nicht noch ein zweites Mal vorkommen. Bei der 5 im Zielfeld können wir die 5 in allen anderen Feldern der fünften Zeile streichen. Dann würden wir die 5 allerdings im Block links überall streichen müssen. Das ist ein Widerspruch, da die 5 in einem der drei noch offenen Felder stehen muss. Also kann im Startfeld nicht die 5 stehen, da es ansonsten kein korrektes Sudoku wäre.
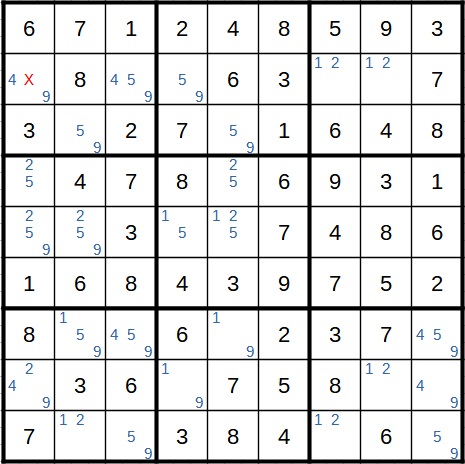
Anschließend noch ein zweites Beispiel. Auch hier sind die Felder wieder gelb markiert. Unser Startfeld ist das gelbe Feld ganz links.
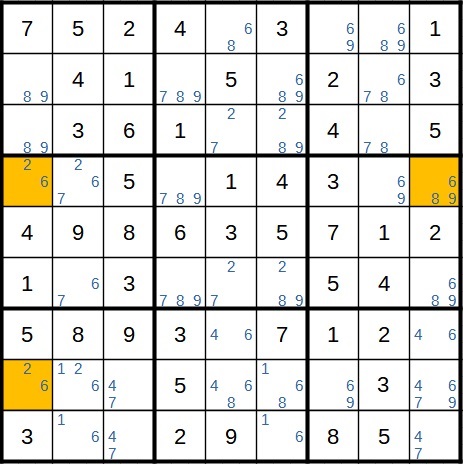
Steht im Startfeld eine 6, haben wir im gelben Feld links in dieser Zeile eine 2. Daraus folgt im Zielfeld weiter unten eine 6.

Hier gilt wieder die gleiche Logik wie oben. Wenn im Startfeld eine 6 steht, haben wir die 6 auch im Zielfeld. Daraus würde aber für den Block unten rechts folgen, dass dort jede 6 als Kandidat wegfällt. Wir sind erneut auf einen Widerspruch gestoßen. Also können wir die 6 im Startfeld wegstreichen.
Wie geht man nun am besten vor, um eine solche Situation zu erkennen? Ich mache es folgendermaßen: Ich suche mir einen Block, in dem ein Kandidat in einer Zeile und einer Spalte jeweils zweimal vorkommt (wie in den Beispielen oben). Dann gehe ich diese Zeile und diese Spalte entlang und halte Ausschau nach Feldern, die diesen Kandidaten ebenfalls enthalten. Eventuell kann man in einem dieser Felder dann auf einen Widerspruch stoßen.
