Sudoku Beispiel 2 (fortgeschritten)

In diesem Sudoku mit fortgeschrittener oder mittelschwerer Schwierigkeitsstufe wird eigentlich nur eine fortgeschrittene Sudoku-Strategie genutzt. Die aber gleich mehrfach in einem Schritt. Es handelt sich hierbei um mehrere direkte zweifache Kandidaten.

Zu Beginn sieht das Sudoku wie folgt aus.

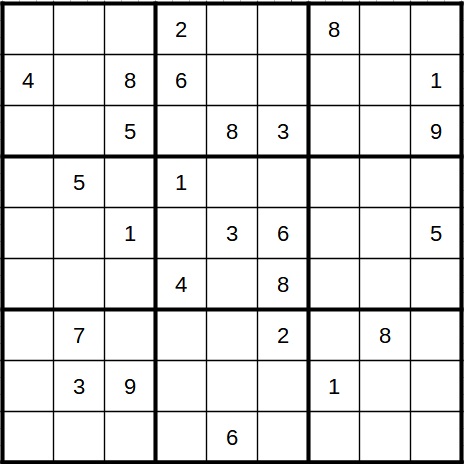
Anschließend können wir einige Zahlen eintragen, auch wenn manche davon knifflig zu sehen sind. Es handelt sich hier zwar um eindeutige Kandidaten, manche davon sind aber versteckt. Diese Schritte überspringe ich hier, da ich mich auf die fortgeschrittene Strategie konzentrieren will. Nachdem die mehr oder weniger eindeutigen Ziffern eingetragen sind, können wir mit der Kandidatenschreibweise fortfahren. Das Bild sieht anschließend folgendermaßen aus.

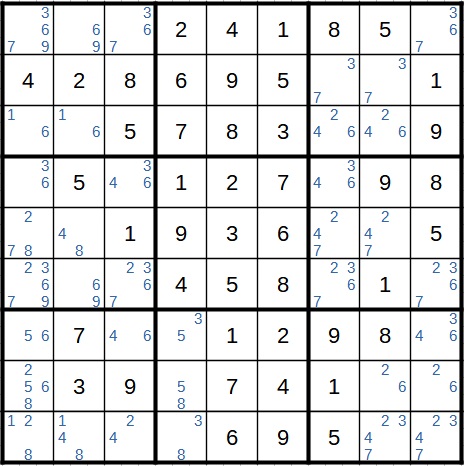
Wenn man sich das Spielfeld jetzt genauer anschaut, erkennt man wie gesagt direkte doppelte Kandidaten. Nämlich ganze vier Stück davon. Drei davon liegen direkt nebeneinander, das vierte Paar (6 und 9 in Spalte 2) liegt etwas weiter auseinander, weshalb ich es in einer anderen Farbe markiert habe.

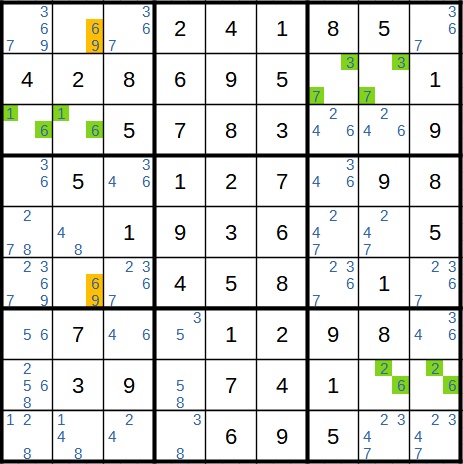
Durch diese Paare fallen einige Kandidaten weg, wie wir im nächsten Schritt sehen werden.

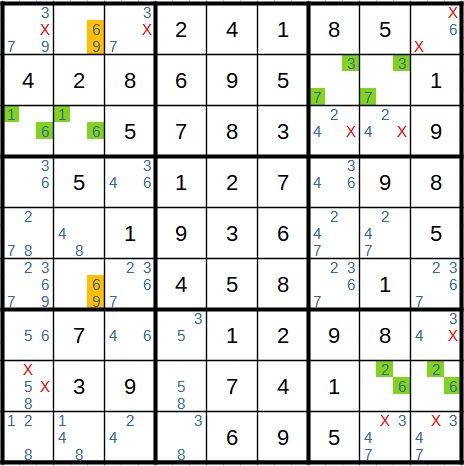
Neben den weggefallenen Kandidaten (durch rotes X gekennzeichnet) gibt es jetzt aber noch eine kuriose Situation. Da das Paar 6/9 in Spalte 2 und 1/6 im Block links oben beide die 6 enthalten, und beide sich überschneiden, heben sich beide Paare sozusagen gegenseitig auf. Im Block links oben haben wir die 1 und die 6 als Paar. Damit fällt im gleichen Block überall sonst die 6 weg. Und dazu gehört auch die 6/9 im gleichen Block, die Teil des anderen Paares ist. Also bleibt dort nur die 9. Auf der anderen Seite liegt in der gleichen Spalte wie 6/9 das Feld mit der 1/6, weshalb dort die 6 wegfällt und die 1 übrig bleibt.

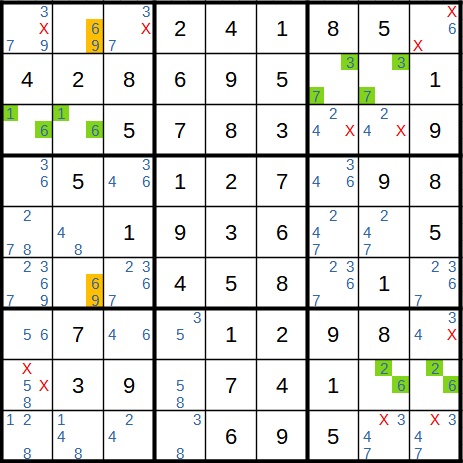
Mit den ganzen weggefallenen Kandidaten bleibt jetzt in einigen Feldern nur noch ein Kandidat übrig. Nachdem dieser jeweils eingetragen wurde, bleibt wiederum in anderen Feldern nur noch ein Kandidat, und immer so weiter. Bis zum Ziel gibt es keine Schwierigkeiten mehr. Die Lösung sieht wie folgt aus:

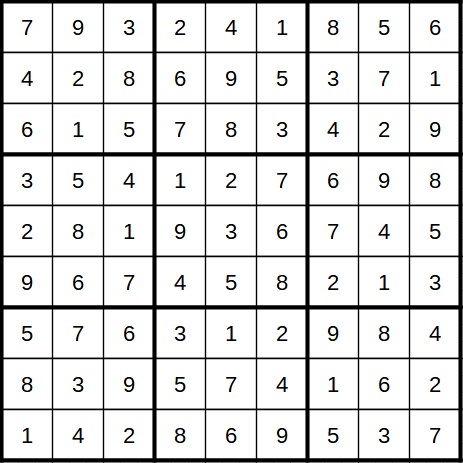
Natürlich hätte man aus dem einen Schritt auch mehrere machen können, indem man jeden Zwilling nacheinander betrachtet und die entsprechenden Kandidaten gestrichen hätte. So wäre es übersichtlicher gewesen.